Matemática Financeira

Juro

A matemática financeira trata, em essência, do estudo do valor do dinheiro ao longo do tempo. O seu objetivo básico é o de efetuar análises e comparações dos vários fluxos de entrada e saída de dinheiro de caixa verificados em diferentes momentos.

Receber uma quantia hoje ou no futuro não são evidentemente a mesma coisa. Em princípio, uma unidade monetária hoje é preferível à mesma unidade monetária disponível amanhã. Postergar uma entrada de caixa (recebimento) por certo tempo envolve um sacrifício, o qual deve ser pago mediante uma recompensa, definida pelos juros. Desta forma, são os juros que efetivamente induzem o adiamento do consumo, permitindo a formação de poupanças e de novos investimentos na economia.

Taxas de juros

A taxa de juros é o coeficiente que determina o valor do juro, isto é, a remuneração do fator capital utilizado durante certo período de tempo.
As taxas de juros se referem sempre a uma unidade de tempo (mês, semestre, ano etc.) e podem ser representadas equivalentemente de duas maneiras: taxa percentual e taxa unitária.

Taxa Percentual

$$ J = {$}1{.}000/100\times 20 = $$ $$ J = {$}10{,}00\times 20 = {$}200{,}00$$

O capital de ${$}1{.}000{,}00$ tem dez centos. Como cada um deles rende 20, a remuneração total da aplicação no período é, portanto de ${$}200{,}00.$

A transformação da taxa percentual em unitária se processa simplesmente pela divisão da notação em percentual por 100. Para a transformação inversa, basta multiplicar a taxa unitária por 100.

Taxa Percentual	Taxa Unitária
1,5%	0,015
8%	0,08
17%	0,17
86%	0,86
120%	1,20
1,500%	15,0

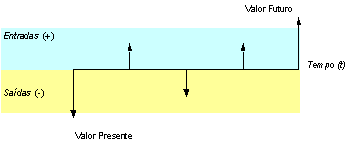
Diagrama do fluxo de caixa

Conforme foi comentado, a matemática financeira se preocupa com o estudo das várias relações dos movimentos monetários que se estabelecem em distintos momentos no tempo.

Estes movimentos monetários são identificados temporariamente através de um fluxo de caixa. O fluxo de caixa é de grande utilidade para as operações de matemática financeira, permitindo que se visualize no tempo o que ocorre com o capital. esquematicamente, pode ser apresentado da forma seguinte:

A linha horizontal registra a  escala de tempo, ou seja, o horizonte financeiro da operação. O ponto zero indica o momento inicial e os demais pontos representam os períodos de tempo (datas).

Fórmulas de Juros Simples

$$ J = C\times i\times n$$ onde J = valor dos juros expresso em unidades monetárias; C = Capital. i = taxa de juros, expressa em sua forma unitária; n = prazo. $$C= \frac{J}{i\times n}$$ $$i = \frac{J}{C\times n}$$ $$ n = \frac{J}{C\times i}$$

Exemplo:

1. Um capital de ${$}80{.}000{,}00$ é aplicado à taxa de $2{,}5$% ao mês durante um trimestre. Pede-se determinar o valor dos juros acumulados neste período.
Solução:
$$ J = C\times i\times n$$ $$J= 80{.}000{,}00\times 0{,}025\times 3$$ $$ J = {$}6{.}000{,}00$$

2. Um negociante tomou um empréstimo pagando uma taxa de juros simples de $6$% ao mês durante nove meses. Ao final deste período, calculou em ${$} 270{.}000{,}00$ o total de juros incorridos na operação. Determinar o valor do empréstimo.
Solução:
C=? i = 6% a.m. (0,06) n = 9 meses J = ${$}270{.}000$ $$C= \frac{J}{i\times n}$$ $$ C = \frac{270{.}000}{0{,}06\times 9} = \frac{270{.}000}{0{,}054}= {$} 500{.}000$$

3. Um capital de ${$} 40{.}000{,}00$ foi aplicado num fundo de poupança por 11 meses, produzindo um rendimento financeiro de ${$}9{.}680{,}00$. Pede-se apurar a taxa de juros oferecida por esta operação.

C = ${$}40{.}000{,}00$ i = ? n = 11 meses J = ${$}9{.}680{,}00$ $$ i = \frac{J}{C\times n}$$ $$ i = \frac{{$}9{.}680{,}00}{{$}40{.}000{,}00\times 11} = \frac{9{.}680{,}00}{440{.}000{,}}= $$ 0,022 ou 2,2% ao mês

4.Uma aplicação de ${$}250{.}000{,}00$ rendendo uma taxa de juros de 1,8% ao mês produz, ao final de determinado período juros no valor de ${$}27{.}000{,}00$. Calcular o prazo da aplicação.

C = ${$}250{.}000{,}00$ i = $1{,}8$% ao mês ${(}0{,}018{)}$ n = ? $J={$}27{.}000{,}00$ $$n=\frac{J}{C\times i}= \frac{27{.}000}{250{.}000\times 0{,}018}= \frac{27{.}000}{4{.}500}= 6\ {meses}$$

Montante e Capital

Um determinado capital, quando aplicado a uma taxa periódica de juro por determinado tempo, produz um valor acumulado determinado de montante, e identificado em juros simples por M. Em outras palavras, o montante é constituído do capital mais o valor acumulado dos juros, isto é:
$$M = C + J$$
No entanto, sabe-se que: $J = C\times i\times n$. Substituindo esta expressão básica na fórmula do montante supra, e colocando-se C em evidência:
$$M = C + C\times i\times n$$ $$M = C(1+i\times n)$$
A expressão $\left(1 + i \times n\right)$ é definida como fator de capitalização (ou de valor futuro -CFS) dos juros simples. Ao multiplicar um capital por este fator, corrige-se o seu valor para uma data futura, determinando o montante. O inverso, ou seja, $\frac{1}{1+i\times n}$ é denominado de fator de atualização (ou de valor presente FAS). Ao se aplicar o fator sobre um valor expresso em uma data futura, apura-se o seu equivalente numa data atual.


Exemplos
1. Uma pessoa aplica ${$} 18{.}000{,}00$ à taxa de 1,5% ao mês durante 8 meses. Determinar o valor acumulado ao final deste período.
Solução:
$C ={$}18{.}000{,}00$
i = 1,5% ao mês (0,015)
n = 8 meses
M = ? $$ M = C(1+i\times n)$$ $$ M = {$} 18{.}000{,}00 (1 + 0{,}015\times 8)$$ $$ M = 18{.}000\times 1{,}12 = {$}\ 20{.}160{,}00$$

Taxa proporcional e taxa equivalente

Por exemplo, para uma taxa de juros de 18% ao ano, se a capitalização for definida mensalmente (ocorrerão 12 vezes juros no período de um ano), o percentual de juros que incidirá sobre o capital a cada mês será:
$$Taxa Proporcional = \frac {18\%}{12}=1{,}5\%\ ao\ mês$$
As taxas de juros simples se dizem equivalentes quando, aplicadas a um mesmo capital e pelo mesmo intervalo de tempo, produzem o mesmo volume linear de juros.
Por exemplo, em juros simples, um capital de ${$}500{.}000{,}00$, se aplicado a 2,5% ao mês ou 15% ao semestre pelo prazo de um ano, produz o mesmo montante linear de juros. Isto é:
$$J(2,5\% a.m.) = {$}500{.}000{,}00\times 0{,}025\times 12 = {$}150{.}000{,}00$$ $$J(15\% a.s.) = {$}500{.}000{,}00\times 0{,}15\times 2 = {$} 150{.}000{,}00$$

Exemplos:

1. Calcular a taxa anual proporcional a: (a) 6% ao ano; (b) 10% ao bimestre.
Solução:
$$ a) i = 6\%\times 12 = 72\%\ ao\ ano$$ $$ b) i = 10\%\times 6 = 60\%\ ao\ ano$$

2. Calcular a taxa de juros semestral proporcional a: (a) 60% ao ano; (b) 9% ao trimestre.
Solução:
$$a) i = \frac{60\%}{12}\times 6 = 30\%\ a.s. \quad pois: \frac{12}{6} = \frac{60}{30}$$ $$\frac{12}{6} = \frac{60}{i}$$ $$ 12i = 60\times 6$$ $$12i = 360$$ $$i = 30$$ $$b) i = \frac{9\%}{3}\times 6 = 18\%\ a.s. \quad ou: i = 9\%\times 2 = 18\%\ a.s.$$

Juro Exato e Juro Comercial

É comum nas operações de curto prazo, onde predominam as aplicações com taxas referenciadas em juros simples, ter-se o prazo definido em número de dias. Nesses casos, o número de dias pode ser calculado de duas maneiras:
a) pelo tempo exato, utilizando-se efetivamente o calendário do ano civil (365 dias). O juro apurado desta maneira denomina-se juro exato;
b) pelo ano comercial, o qual admite o mês com 30 dias e o ano com 360 dias. Tem-se por este critério, a apuração do denominado juro comercial ou ordinário.
Por exemplo, 12% ao ano equivale, pelos critérios enunciados, à taxa diária de:
a) Juro Exato: $$ \frac {12\%}{365 dias} = 0{,}032877\% ao\ dia$$
b) Juro Comercial:$$ \frac {12\%}{360\ dias} = 0{,}033333\%\ ao\ dia$$
Na ilustração, o juro comercial diário é ligeiramente superior ao exato pelo menor número de dias considerado no intervalo de tempo.

Equivalência Financeira

O problema da equivalência financeira constitui-se no raciocínio básico da matemática financeira. Conceitualmente, dois ou mais capitais representativos de uma certa data dizem-se equivalentes quando, a uma certa taxa de juros, produzem resultados iguais numa data comum.
Por exemplo, ${$}120{,}00$ vencíveis daqui a um ano e ${$}100{,}00$, hoje, são equivalentes a uma taxa de juros simples de $20\%$, uma vez que os ${$}100{,}00$ capitalizados, produziriam ${$}120{,}00$ dentro de um ano, ou os ${$}120{,}00$, do final do primeiro ano, resultariam em ${$}100{,}00$ se atualizados para hoje. Ou seja, ambos os capitais produzem, numa data de comparação (data focal) e taxa de $20\%$ ano ano, resultados idênticos.
Exemplos: 1. Determinar se ${$}438{.}080{,}00$ vencíveis daqui a 8 meses é equivalente se receber hoje ${$}296{.}000{,}00$, admitindo uma taxa de juros simples de $6\%$ ao mês.
Solução:
Data Focal = 8 $$M= 296{.}000\times (1 + 0{,}06\times 8)$$
Data Focal = 0(zero):
$$C=\frac{438{.}080{,}00}{(1+0{,}06\times 8)}$$
Os capitais são equivalentes à taxa de $6\%$ ao mês. Portanto, a esta taxa de juros é indiferente receber ${$}296{.}000{,}00$ hoje ou $438{.}080{,}00$ daqui a 8 meses.

Os capitais A1, A2 e B1, B2 e B3 dizem-se equivalentes se, quando expressos em valores de uma data comum (data de comparação ou data focal), e a mesma razão de juros, apresentam resultados iguais. Sendo a data de comparação o momento $0$, tem-se:
$$\frac{A1}{(1+i\times 1)}+ \frac{A2}{(1+i\times 2)}=\frac{B1}{(1+i\times 3)}+\frac{B2}{(1+i\times 4)}+\frac{B3}{(1+i\times 5)}$$

Juros Compostos

O regime de juros compostos considera que os juros formados em cada período são acrescidos ao capital formando o montante (capital mais juros) do período. Este montante, por sua vez, passará a render juros no período seguinte formando um novo montante (constituído do capital inicial, dos juros acumulados e dos juros sobre os juros formados em períodos anteriores), e assim por diante. Este processo de formação dos juros é diferente daquele descrito para os juros simples, onde unicamente o capital rende juros, não ocorrendo remuneração sobre os juros formados em períodos anteriores. Tecnicamente o regime de juros compostos é superior ao de juros simples, principalmente pela possibilidade de fracionamento dos prazos, conforme foi introduzido no capítulo anterior. No critério composto, a equivalência de capitais pode ser apurada em qualquer data, retratando melhor a realidade das operações que o regime linear.

Fórmulas de juros compostos

Para melhor desenvolver este conceito e definir suas fórmulas de cálculo, admita ilustrativamente uma aplicação de ${$}1{.}000{,}00$ a taxa composta de $10\%$ ao mês. Identificando-se por PV o valor presente (capital) e FV o valor futuro (montante), tem-se os seguintes resultados ao final de cada período:

Final do 1º mês: o capital de ${$}1{.}000{,}00$ produz resultados de ${$}100{,}00$ ($10\%\times {$}1{.}000)$ e um montante de ${$}1{.}100{,}00 (1{.}000{,}00 + 100{,}00)$, ou seja:
$$FV = 1{.}000{,}00\times (1 + 0{,}010)= {$}1{.}100{,}00$$

Final do 2º mês: o montante do mês anterior ${$}1{.}100{,}00$ é o capital deste 2º mês, servindo de base para o cálculo de juros deste período. Assim:

$$FV= 1{.}000{,}00\times (1+0{,}10)\times (1+0{,}10)$$ $$FV = 1{.}000{,}00\times (1+0{,}10)^2 = {$}1{.}210{,}00$$

Generalizando:
$$FV = PV\times(1+i)^n$$ $$PV = \frac{FV}{(1+i)^n}$$

Onde $(1+i)^n$ é o fator de capitalização (ou de valor futuro), - FCC(i,n) a juros compostos, e $\frac{1}{(1+i)^n}$ o fator de atualização (ou de valor presente) - FAC(i,n) a juros compostos.

Por outro lado, sabe-se que o valor monetário dos juros (J) é apurado pela diferença entre o montante (FV) e o capital (PV), podendo-se obter seu resultado também pela seguinte expressão: $$J = FV - PV$$

Como: $FV = PV(1+i)^n$
Colocando-se PV em evidência:
$$J = PV\times [(1+i)^n - 1]$$

Exemplo: 1. Se uma pessoa deseja obter ${$}27{.}500{,}00$ dentro de um ano, quanto deverá ela depositar hoje numa alternativa de poupança que rende $1{,}7\%$ de juros compostos ao mês?
Solução:
FV = ${$}27{.}500{,}00$ n = 1 ano (12 meses); i = 1,7% ao mês PV = ? $$PV = \frac{FV}{(1+i)^n}= \frac{27{.}500{,}00}{(1+0{,}017)^{12}}= \frac{27{.}500{,}00}{(1{,}017)^{12}}$$ $$PV = \frac{27{.}500{,}00}{1{,}224197}= {$} 22{.}463{,}70$$
De fato, uma aplicação de ${$}22{.}463{,}70$ hoje, a $1{,}7\%$ a.m. de juros compostos, produz ao final de um ano o montante de ${$}27{.}500{,}00$, ou seja:
$$FV = 22{.}463{,}70\times (1{,}017)^{12}= {$} 27{.}500{,}00$$

2. Qual o valor de resgate de uma aplicação de ${$}12{.}000{,}00$ em um título pelo prazo de 8 meses à taxa de juros composta de $3,5\%$ a.m.?
Solução:
$$FV= PV(1+i)^n = 12{.}000\times(1+0{,}035)^8 = 12{.}000\times 1{,}316809 = {$} 15{.}801{,}71$$
3. Determine a taxa mensal composta de uma aplicação de ${$}40{.}000{,}00$ que produz um montante de ${$}43{.}894{,}63$ ao final de um quadrimestre.
Solução:
$$FV = PV(1+i)^n$$ $$\frac{FV}{PV}=(1+i)^4$$ $$\frac{43{.}894{,}63}{40{.}000{,}00}=(1+i)^4$$ $$1{,}097366 = (1+i)^4$$ $$\sqrt[4]{1{,}097366}= \sqrt[4]{(1+i)^4}$$ $$1+i = 1{,}0235$$ $$i = 0{,}0235\ ou\ 2{,}35\% {a.m.}$$

4. Uma aplicação de ${$}22{.}000{,}00$ efetuada em certa data produz, à taxa composta de juros de $2{,}4\%$ ao mês, um montante de ${$}26{.}596{,}40$ em certa data futura. Calcular o prazo da operação.
$$FV = PV(1+i)^n$$ $$\frac{FV}{PV}=(1+i)^n$$ $$\frac{26{.}596{,}40}{22{.}000{,}00}=(1{,}024)^n$$ $$1{,}208927 = (1{,}24)^n$$
Aplicando logaritmos, tem-se:
$${log} 1{,}208927 = n\times {log} 1{,}024$$ $$n = \frac{{log}1{,}208927}{{log}1{,}024}= \frac{0{,}082400}{0{,}010300}= 8\ {meses}$$

Taxas Equivalentes

Ao se tratar de juros simples, foi comentado que a taxa equivalente é a própria taxa proporcional da operação. Por exemplo, a taxa de $3\%$ ao mês e $9\%$ ao trimestres são ditas proporcionais, pois mantêm a seguinte relação:
$$\begin{matrix} \underbrace{ \frac{1}{3} } \\ {Prazos} \end{matrix}= \begin{matrix} \underbrace{ \frac{3}{9} } \\ {Taxas}\end{matrix}$$
São também equivalentes, pois promovem a igualdade dos montantes de um mesmo capital ao final de certo período de tempo. Por exemplo, em juros simples um capital de ${$}80{.}000{,}00$ produz o mesmo montante em qualquer data se capitalizado a $3\%$ a.m. e $9\%$ a.t.


$$n = 3 meses \begin{cases} FV(3\%{a.m.}) = 80{.}000{,}00(1+0{,}03\times 3) = {$}87{.}200{,}00 \\ FV(9\%{a.t.})= 80{.}000{,}00(1+0{,}09\times 1) = {$}87{.}200{,}00 \end{cases}$$
$$n= 12 meses \begin{cases} FV(3\%{a.m.}) = 80{.}000{,}00(1+0{,}03\times 12) = {$}87{.}200{,}00 \\ FV(9\%{a.t.})= 80{.}000{,}00(1+0{,}09\times 4) = {$}87{.}200{,}00 \end{cases}$$
O conceito enunciado de taxa equivalente permanece válido para o regime de juros compostos diferenciando-se, no entanto, a fórmula de cálculo da taxa de juros. Por se tratar de capitalização exponencial, a expressão da taxa equivalente composta é a média geométrica da taxa de juros do período inteiro, isto é:
$$i_q= \sqrt[q]{1+i}-1$$
onde: q = número de períodos de capitalização.
Exemplo: A taxa equivalente composta mensal de $10{,}3826\%$ é de $1{,}66\%$ ou seja:
$$i_6= \sqrt[6]{1+0{,}103826}-1$$ $$i_6= \sqrt[6]{1{,}103826}-1 = 1{,}0166-1 = 0{,}0166\ ou\ 1{,}66\% {a.m.}$$

Taxa nominal e taxa efetiva

A taxa efetiva de juros é a taxa de juros apurada durante todo o prazo n, sendo formada exponencialmente através dos períodos de capitalização. Ou seja, a taxa efetiva é o processo de formação dos juros pelo regime de juros compostos ao longo dos períodos de capitalização. É obtida pela seguinte expressão:
$${Taxa\ Efetiva}({i_f}) = (1+i)^q -1$$
onde q representa o número de períodos de capitalização dos juros.
Por exemplo, uma taxa de $3{,}8\%$ ao mês determina um montante efetivo de juros de $56,45\%$ ao ano, ou seja:
$${Taxa\ Efetiva}({i_f}) = (1+i)^q -1$$ $$i_f = (1+0{,}038)^{12}-1 = 56{,}44\% {a.a.}$$

Descontos

Entende-se por valor nominal o valor de resgate, ou seja, o valor definido para um título em sua data de vencimento. Representa, em outras palavras, o próprio montante da operação.
A operação de se liquidar um título antes de seu vencimento envolve geralmente uma recompensa, ou um desconto pelo pagamento antecipado. Desta maneira, desconto pode ser entendido como a diferença entre o valor nominal de um título e o seu valor atualizado apurado n períodos antes de seu vencimento.
Por outro lado, o valor descontado de um título é o seu valor atual na data do desconto, sendo determinado pela diferença entre o valor nominal e o desconto, ou seja:
Valor Descontado = Valor Nominal - Desconto

As operações de desconto podem ser realizadas tanto sob o regime de juros simples como no de juros compostos.

Descontos Racionais (ou "por dentro")

O desconto racional, também denominado de desconto "por dentro", incorpora os conceitos e relações básicas de juros simples, conforme desenvolvidos no primeiro capítulo.
Assim, sendo $D_ r$ o valor do desconto racional, C o capital (ou valor atual), i a taxa periódica de juros e n o prazo do desconto (número de períodos que o título é negociado antes de seu vencimento), tem-se a conhecida expressão de juros simples:
$$D_r=C\times i\times n$$
Pela própria definição de desconto e introduzindo-se o conceito de valor descontado no lugar de capital no cálculo do desconto, tem-se:
$$D_r=N-V_r$$
sendo N o valor nominal (ou valor de resgate, ou montante) e $V_r$ o valor descontado (ou valor atual) na data da operação. Como:
$$V_r=C= \frac{N}{1+i\times n}$$
tem-se:
$$D_r=N- \frac{N}{1+i\times n}=\frac{N(1+i\times n)-N}{1+i\times n}= \frac{N+N\times i\times n-N}{1+i\times n}$$ $$D_r= \frac{N\times i\times n}{1+i\times n}$$
Já o valor descontado, conforme definição apresentada, é obtido pela seguinte expressão de cálculo:

$$V_r=N-D_r$$ $$V_r=N- \frac{N\times i\times n}{1+i\times n}$$ $$V_r = \frac{N(1+i\times n)-N\times i\times n}{1+i\times n}$$ $$= \frac{N+N\times i\times n - N\times i\times n}{1+i\times n}$$
$$V_r = \frac{N}{1+i\times n}$$

Observe, uma vez mais, que o desconto racional representa exatamente as relações de juros simples descritas no capítulo inicial. É importante registrar que o juro incide sobre o capital (valor atual) do título, ou seja, sobre o capital liberado da operação. A taxa de juro (desconto) cobrada representa, dessa maneira, o custo efetivo de todo o período do desconto.

Exemplos:
1. Seja um título de valor nominal de $4{.}000{,}00$ vencível em um ano, que está sendo liquidado 3 meses antes de seu vencimento. Sendo de $42\%$ a.a. a taxa nominal de juros corrente, pede-se calcular o desconto e o valor descontado desta operação.

Solução:
Desconto

$$D_r= \frac{N\times i\times n}{1+i\times n}$$ $$D_r= \frac{4{.}000\times 0{,}035\times 3}{1+0{,}035\times 3}= \frac{420{,}00}{1{,}105}={$}380{,}00$$

Valor Descontado
$$V_r= N-D_r$$ $$V_r = 4{.}000{,}00-380{,}10 = {$}3{.}619{,}90$$
Ou:
$$V_r = \frac{N}{1+i\times n}= \frac{4{.}000{,}00}{1+0{,}035\times 3}= {$}3{.}619{,}90$$

Do ponto de vista do devedor $380{,}10$ representam o valor que está deixando de pagar por saldar a dívida antecipadamente (3 meses antes de seu vencimento). O valor líquido do pagamento (valor descontado) é de $3{.}619{,}90$

Desconto bancário (ou comercial, ou "por fora")

Este tipo de desconto, simplificadamente por incidir sobre o valor nominal (valor de resgate) do título, proporciona maior volume de encargos financeiros efetivos nas operações. Observe que, ao contrário dos juros "por dentro", que calculam os encargos sobre o capital efetivamente liberado na operação, ou seja, sobre o valor presente, o critério "por fora" apura os juros sobre o montante, indicando custos adicionais ao tomador de recursos.
A modalidade de desconto "por fora" é amplamente adotada pelo mercado, notadamente em operações de crédito bancário e comercial a curto prazo.
O valor deste desconto, genericamente denominado desconto "por fora" $(D_f)$, no regime de juros simples é determinado pelo produto do valor nominal do título (N), da taxa de desconto periódica "por fora" contratada na operação (d) e do prazo de antecipação definido para o desconto (n). Isto é:

$$D_F = N\times d\times n$$

O valor descontado "por fora" $(V_F)$, aplicando-se a definição, é obtido:

$$V_F=N-D_F$$ $$V_F = N-N\times d\times n\qquad \longrightarrow V_F = N(1-d\times n)$$
Exemplo:
1. Seja um título de valor nominal de ${$}4{.}000{,}00$ vencível em um ano, que está sendo liquidado antes de seu vencimento. Sendo de $42\%$ a.a. a taxa de desconto adotada, pede-se calcular o desconto e o valor descontado desta operação.
Solução:

Desconto
$$D_F=N\times d\times n$$ $$D_F= 4{.}000{,}00\times 0{,}035\times 3 \qquad \longrightarrow D_F = 420{,}00$$
Observe que o maior valor dos juros cobrado pelo título deve-se ao fato, conforme ressaltado anteriormente, de o desconto "por fora" ser aplicado diretamente sobre o valor nominal (valor de resgate) e não sobre o valor atual como é característico das operações de desconto racional.

Em verdade, o valor do desconto "por fora" aquivale, num mesmo momento do tempo, ao montante do desconto "por dentro", supondo-se as mesmas condições de prazo e taxa. Isto é:

$$D_r = {$}380{,}10$$ $$D_F = {$}420{,}00$$

Para uma taxa de $3{,}5\%$ a.m. e um período de desconto de 3 meses, conforme estabelecido na ilustração, tem-se:

$$D_F = D_r(1+i\times n)$$ $$D_F= 380{,}10\times(1+0{,}035\times 3) = 380{,}00\times (1{,}105) \longrightarrow D_F = {$}420{,}00$$

O cálculo do valor descontado $(V_F)$ é desenvolvido:

$$V_F = N(1-d\times n)$$ $$V_F = 4{.}000{,}00\times(1-0{,}035\times 3)$$ $$V_F = 4{.}000{,}00\times (0{,}895) \\ V_F = {$}3{.}580{,}00$$

Torna-se evidente que o devedor desse título, descontado pelo desconto bancário (ou comercial, ou "por fora"), assume encargos maiores que aqueles declarados para a operação.

A taxa de juros efetiva desta operação não equivale à taxa de desconto utilizada. Note que, se são pagos ${$}420{,}00$ de juros sobre um valor atual de ${$}3{.}580{,}00$, a taxa de juros assume o seguinte percentual efetivo:

$$i = \frac{{$}420{,}00}{{$}3{.}580{,}00}= 11{,}73\%\quad {ao\ trimestre}$$

Inflação

Em ambientes inflacionários é indispensável, para o correto uso das técnicas da Matemática Financeira, ressaltar, nas várias taxas de juros nominais praticadas na economia, o componente devido à inflação e aquele declarado como real. A parte real é aquela obtida livre das influências da taxa de depreciação monetária verificada, isto é, adicionalmente à inflação.
De maneira simplista, o processo inflacionário de uma economia pode ser entendido pela elevação generalizada dos preços dos vários bens e serviços.
Em sentido contrário, diante de uma baixa predominante dos preços de mercado dos bens e serviços, tem-se o fenômeno definido por deflação.

Índices de preços

Um índice de preços é resultante de um procedimento estatístico que, entre outras aplicações, permite medir as variações ocorridas nos níveis gerais de preços de um período para outro. Em outras palavras, o índice de preços representa uma média global das variações de preços que se verificaram num conjunto de determinados bens ponderada pelas quantidades respectivas.

MÊS	Maio	Junho	Julho	Agosto	Setembro	Outubro	Novembro	Dezembro
IGP	649,79	703,38	800,31	903,79	1.009,67	1.152,63	1.353,79	1.576,56

Pela evolução desses índices de preços pode ser constatado como os preços gerais da economia variaram no período. Para tanto, relaciona-se o índice do fim do período que se deseja estudar com o do início.

Por exemplo, a taxa de inflação do 2º semestre medida pelo IGP está refletida na evolução apresentada entre o índice de junho (início do semestre) e o de dezembro (fim do semestre). Assim:
$${{Inflação}\ do\ 2º semestre} = \frac{1{.}576{,}56}{703{,}38}-1 = 2{,}2414-1= 124{,}14\%$$
Os preços nesse período cresceram 2,2414 vezes, indicando uma evolução de 124,14%.

A inflação do trimestre out./dez., seguindo o mesmo raciocínio, é medida da forma seguinte:
$$\frac{1{.}576{,}56}{1{.}009{,}67}-1 = 56{,}15\%$$

Dessa maneira, a taxa de inflação, a partir de índices de preços, pode ser medida pela seguinte expressão:

$$I=\frac{P_{n}}{P_{n-t}}-1$$

Exemplos:
1. Abaixo são transcritos alguns valores divulgados do IGP-di e do INPC (Índice Nacional de Preços ao Consumidor). Com base nestes resultados, pede-se:
a) Calcular a taxa de inflação, medida pelo IGP e INPC, para os seguintes períodos de 20X3:
- Ano
- 1º semestre
- Mês de dezembro;

b) um bem que custava ${$}5{.}000{,}00$ no início do ano, quanto deve valer ao final deste ano se for corrigido pela variação do IGP e INPC;

c) Admitindo que o proprietário tenha vendido este imóvel ao final do ano por ${$}90{.}000{,}00$, determinar o lucro auferido.

	Dez./X2	Jun./X3	Nov./X3	Dez./X3
IGP-di	100,00	708,38	1.353,79	1.576,56
INPC	5,9341	43,4599	83,9349	100,0

Solução:

a) Taxa de Inflação - I

	IGP	INPC
ANO	(1.576,56/100,00)-1=1.476,56%	(100,0/5,9341)-1=1.585,18%
1º semestre	(708,38/100,0)-1=608,38%	(43,5499/5,9341)-1=632,38%
Dezembro	(1.576,56/1.353,79)-1=16,46%	(100,0/83,9349)-1=19,14%

b) Valor Corrigido do Imóvel

Pelo IGP:
$$5{.}000{,}00 \frac{1{.}576{,}56}{100{,}00}= {$}78{.}828{,}00$$

Pelo INPC:
$$5{.}000{,}00 \frac{100{,}00}{5,9341}={$}84{.}258{,}80$$

c) O lucro pode ser avaliado sob duas formas: o nominal, medido pela simples diferença entre o valor de venda e o de compra, e o real, apurado adicionalmente à inflação.

No caso em questão, o proprietário vendeu o imóvel apurando lucro real, isto é, o preço de venda excedeu ao valor de compra corrigido. Assim, pelo IGP, apura-se um lucro real de: ${$}90{.}000{,}00 - {$}78{.}828{,}00 = {$}11{.}172{,}00$ e pelo INPC, o lucro real foi menor: ${$} 90{.}000{,}00 - {$}84{.}258{,}80 = {$}5{.}741{,}20$.

Taxa de Desvalorização da Moeda

Enquanto a inflação representa uma elevação nos níveis de preços, a taxa de desvalorização da moeda (TDM) mede a queda no poder de compra da moeda causada por estes aumentos de preços.
Por exemplo, se em determinado período os preços em geral dobraram (inflação de 100%), conclui-se que a capacidade de compra das pessoas reduziu-se em 50%, ou seja, somente podem adquirir a metade do que costumavam consumir no passado. Diz-se, em outras palavras, que a capacidade aquisitiva da moeda diminuiu em 50%

A taxa de desvalorização da moeda (TDM), para diferentes taxas de inflação, pode ser obtida a partir da seguinte fórmula:

$$TDM = \frac{I}{1+I}$$
Sendo I a taxa de inflação do período.
Por exemplo, se em determinado período a taxa de inflação alcançar a 8%, a queda na capacidade de compra registra a marca de $7{,}4\%$, isto é:

$$TDM = \frac{0{,}08}{1+0{,}08}= \frac{0{,}08}{1{,}08}=7{,}4\%$$

A inflação de 8% determina uma redução do poder de compra da moeda igual a 7,4%, isto é, com este percentual de evolução dos preços as pessoas adquirem 7,4% a menos de bens e serviços que costumam consumir.
Quanto maior a inflação, evidentemente maior será a taxa de desvalorização da moeda definindo em consequência uma menor capacidade aquisitiva.

Outro exemplo permite uma melhor compreensão das taxas de inflação e de desvalorização da moeda.
Admita que a inflação em determinado período tenha alcançado a taxa de $40\%$. Este percentual indica uma queda na capacidade de compra geral de $28{,}6\%$ $(0,4/1,4)$ ou, o que é o mesmo, ao final do período somente podem ser consumidos $71{,}4\%$ dos bens e serviços originais. Para que o poder de compra se mantenha inalterado, as rendas das pessoas devem ser corrigidas por $40\%$, que corresponde à inflação verificada o período.
Para um salário de, por exemplo ${$}1{.}000{,}00$, o reajuste para manter inalterado o poder de compra deve atingir $40\%$ passando o seu valor para ${$}1{.}400{,}00$.
Se for atribuído um reajuste salarial de $50\%$, o assalariado obtém um ganho real em suas rendas, isto é, uma correção acima da inflação. Assim, seu salário se eleva para ${$}1{.}500{,}00$, que representa um reajuste adicional à inflação de ${$}100{,}00$, ou: $[({$}1{.}500{,}00/{$}1{.}400{,}00)-1]= 7{,}14\%$

Um reajuste salarial exatamente igual à inflação de $40\%$ preserva o poder aquisitivo constante. O salário passa para ${$}1{.}400{,}00$ indicando que, em média, pode ser adquirido ao final do período o mesmo montante de bens e serviços consumidos no início.

Uma correção de $25\%$ nos salários, por outro lado, denota uma perda no poder de compra, reduzindo o ingresso de recursos em valores reais, em $150{,}00: [({$}1{.}000{,}00\times 1{,}25)-{$}1{.}400{,}00]$. Esta correção nominal dos salários menor que a inflação equivale a uma perda real de $10{,}7\%$ $[({$}1{.}250{,}00/{$}1{.}400{,}00)-1]$.

Exemplos
1. Admita que em determinado período a inflação tenha atingido $10{,}6\%$. Determinar:
a) Reposição salarial necessária para que um assalariado mantenha a mesma capacidade de compra;
b) Redução do poder aquisitivo do assalariado, supondo que os seus vencimentos não sofrearam reajuste no período.

Solução

a)A reposição salarial para manutenção do seu poder aquisitivo é a própria taxa de inflação de $10{,}6\%$.
Por refletir o aumento médio dos bens e serviços consumidos na economia, admite-se que a correção dos salários pela taxa de inflação repõe, pelo menos ao nível de uma cesta básica de bens e serviços, a perda da capacidade de compra da moeda.


b) A redução do poder aquisitivo é mensurada pela taxa de desvalorização da moeda, ou seja:
$$TDM = \frac{I}{1+I} = \frac{0{,}106}{1{,}106}= 9{,}58\%$$
Com a elevação de $10{,}6\%$ nos índices de preços, o assalariado passa a ter uma capacidade de compra $9{,}58\%$ menor.

2. Num período de inflação, a moeda perde uma parte de sua capacidade de compra, afetando principalmente aqueles que não obtêm um reajuste em suas rendas. Nestas condições, determinar, para uma pessoa que manteve inalterado o seu salário no período, quanto pode adquirir ao final do mês daquilo que consumia no início. Considere uma inflação de $2{,}5\%$ no mês.

Solução
$$TDM = \frac{0{,}025}{1{,}025}= 2{,}4\%$$

A pessoa perdeu $2{,}4\%$ de seu poder de compra, indicando uma capacidade de consumo de $97{,}56\%$ no final do mês do que consumia no início.

3.Uma loja está vendendo suas mercadorias para pagamento em 30 dias sem acréscimo. Sendo de $1{,}8\%$ ao mês a taxa de inflação, determinar o percentual de perda inflacionária motivada pela venda a prazo.

Solução
A perda inflacionária pela venda a prazo está refletida na taxa de desvalorização da moeda, isto é:

$$TDM = \frac{I}{1+I}= \frac{0{,}018}{1{,}018} = 1{,}77\%$$
Em outras palavras, o dinheiro no momento do recebimento estará valendo $1{,}77\%$ a menos, determinado pela taxa de inflação verificada no período.

4. Uma venda de ${$}40{.}000{,}00$ foi efetuada com prazo de pagamento de 40 dias. Sendo de $2\%$ ao mês a inflação, determinar o montante da perda inflacionária desta venda e a taxa de redução do poder de compra do dinheiro.

Solução
$$I = 2\% \mbox{a.m. ou:} \left(\sqrt[30]{1{,}02}\right)^{40}-1 = 2{,}68\% \mbox{p/ 40 dias}$$

Taxa nominal e taxa real

A taxa nominal de juros é aquela adotada normalmente nas operações correntes de mercado, incluindo os efeitos inflacionários previstos para o prazo da operação. Constitui-se em outras palavras, numa taxa prefixada de juros, que incorpora as expectativas da inflação.
É importante separar claramente a taxa nominal de juros, que mede o resultado de uma operação em valor corrente, da taxa nominal (linear) estudada nos primeiros capítulos, que indica a descapitalização do juro de forma proporcional (juros simples).

Em contexto inflacionário, ainda devem ser identificadas na taxa nominal (prefixada) uma parte devida à inflação, e outra definida como legítima, real, que reflete "realmente" os juros que foram pagos ou recebidos.

O objetivo do cálculo da taxa real (r) é o de expurgar a indexação da taxa total de juros (nominal), de maneira a expressar o juro real.

Por exemplo, foi publicado que a remuneração das aplicações em determinado título atingiu $12{,}8\%$ num período, sendo de $9{,}2\%$ a taxa de inflação deste intervalo de tempo. Logo, quem aplicou, ilustrativamente, ${$}100{.}000{,}00$ no início do período, obteve um rendimento nominal de ${$}12{.}800{,}00$ $(12{,}8\%\times {$} 100{.}000{,}00)$ no período totalizando um montante de ${$}112{.}800{,}00$.

Por outro lado, para manter inalterado o seu poder de compra, o capital acumulado do aplicador deve atingir ao final do período, a soma de ${$}109{.}200{,}00 \quad ({$}100{.}000{,}00\times 1{,}092)$. Como o valor de resgate soma ${$}112{.}800{,}00$ conclui-se que pela existência de um lucro real, em valores monetários, de ${$}3{.}600{,}00\qquad ({$}112{.}800{,}00-{$}109{.}200{,}00)$. Isto é, o aplicador obteve um ganho real, acima do principal investido corrigido pela inflação, de ${$}3{.}600{,}00$. Tem termos percentuais, o retorno real da operação, determinado pela relação entre o lucro (ganho) e o valor aplicado, ambos expressos em moeda de mesmo poder de compra, é igual a $3{,}3\%$, $({$}3{.}600{,}00/{$}109{.}200{,}00)$.

De uma maneira geral, a fórmula de apuração da taxa real é a seguinte:

$${Taxa\ Real(r) = } \frac{1+{taxa\ nominal (i)}}{1+{taxa\ de\ inflação\ (I)}}-1$$

Substituindo-se os valores do exemplo acima na expressão de cálculo de r, tem-se:

$$r= \frac{1+0{,}128}{1+0{,}092}-1 = \frac{1{,}128}{1{,}092}-1= 3{,}3\%$$
A partir da identidade da taxa real, pode-se calcular a taxa nominal e a taxa de inflação: $$i = (1+r)\times (1+I)-1$$ $$I = \frac{(1+i)}{(1+r)}-1$$

Exemplos:

1. Uma pessoa aplicou ${$}400{.}000{,}00$ num título por 3 meses à taxa nominal de 6,5% a.t. Sendo de 4,0% a inflação deste período, demonstrar os rendimentos nominal e real auferidos pelo aplicador, assim como as respectivas taxas de retorno.

Solução
$${Valor\ de\ Resgate} = {$}400{.}000{,}00\times 1{,}065 = {$}426{.}000{,}00$$ $${Valor\ Aplicado} = (400{.}000{,}00)$$ $${Rendimento \ Nominal:}\ {$}26{.}000{,}00$$ $${Rentabilidade\ Nominal\ (i)=} \frac{{$}26{.}000{,}00}{{$}400{.}000{,}00} = 6{,}5\% \mbox{a.t.}$$
Ou:
$$\sqrt[3]{1{,}065}-1 = 2{,}12\% \mbox{a.m.}$$

- Perda pela Inflação do Trimestre:
$${$}400{.}000{,}00\times 4\% = {$}16{.}000{,}00$$
Rendimento Real (r):
$$\frac{10{.}000}{400{.}000\times 1{,}04} = 2{,}4\% \mbox{a.t.}$$ $${ou:}$$ $$\sqrt[3]{1{,}024}-1 = 0{,}79\% \mbox{a.m.}$$

A taxa real pode ser obtida pelo emprego direto da fórmula:

$$r = \frac{1+i}{1+I}-1 = \frac{1+0{,}065}{1+0{,}04}-1 = 2{,}4\% {a.t.}$$

Correção Monetária

Sistemas de Amortização e Empréstimos e Financiamentos

Os sistemas de amortização são desenvolvidos basicamente para operações de empréstimos e financiamentos de longo prazo, envolvendo desembolsos periódicos do principal e encargos financeiros.
Existem diversas maneiras de se amortizar uma dívida, devendo as condições de cada operação estarem estabelecidas em contrato firmado entre o credor (mutuante) e o devedor (mutuário).
Uma característica fundamental dos sistemas de amortização a serem estudados neste capítulo é a utilização exclusiva do critério de juros compostos, incidindo os juros exclusivamente sobre o saldo devedor (montante) apurado em período imediatamente anterior.
Para cada sistema de amortização é construída uma planilha financeira, a qual relaciona, dentro de uma certa padronização, os diversos fluxos de pagamentos e recebimentos.
São considerados também modalidades de pagamento com e sem carência, conforme estudadas em capítulos anteriores. Na carência, não há pagamento do principal, sendo pagos somente os juros. Eventualmente, os juros podem ser capitalizados durante o prazo de carência.
O capítulo trata dos seguintes sistemas de amortização:
a) Sistema de Amortização Constante - SAC;
b) Sistema de Prestação Constante (SPC) também conhecido por Sistema de Amortização Francês (SAF);
c) Sistema de Amortização Misto (SAM);
d) Sistema de Amortização Americano (SAA);
e) Sistema de Amortizações Variáveis. Parcelas intermediárias.

Definições Básicas

Os sistemas de amortização de empréstimos e financiamentos tratam, basicamente, da forma pela qual e os encargos financeiros são restituídos ao credor do capital.
Antes do estudo desses vários sistemas, é importante que sejam definidos os principais termos empregados nas operações de empréstimos e financiamentos.
- Encargos (Despesas) Financeiros - representam os juros da operação, caracterizando-se como custo para o devedor e retorno para o credor.
Os encargos financeiros podem ser prefixados ou pós-fixados. O que distingue essas duas modalidades é a correção (indexação) da dívida em função de uma expectativa (prefixação) ou verificação posterior (pós-fixação) do comportamento de determinado indexador.
Em outras palavras, nas operações pós-fixadas, há um desmembramento dos encargos financeiros em juros e correção monetária (ou variação cambial, no caso da dívida ser expressa em moeda estrangeira) que vier a se verificar no futuro; e nas prefixadas estipula-se uma taxa única, a qual incorpora evidentemente uma expectativa inflacionária, para todo o horizonte de tempo.
Assim, para uma operação pós-fixada, a taxa de juros contratada é a taxa definida como real, isto é, aquela situada acima do índice de inflação verificado no período.
Além do encargo real da taxa de juros, as operações pós-fixadas preveem também a correção monetária (ou variação cambial) do saldo devedor da dívida, o que representa normalmente a recuperação da perda de poder aquisitivo (desvalorização perante a inflação) da parte do capital emprestado e ainda não restituído.
Nas operações prefixadas, os encargos financeiros são mediados por uma única taxa, a qual engloba os juros exigidos pelo emprestador e a expectativa inflacionária (correção monetária) para o período de vigência.

- Amortização A amortização refere-se exclusivamente ao pagamento do principal (capital emprestado), o qual é efetuado, geralmente, mediante parcelas periódicas (mensais, trimestrais etc.). Alguns poucos tipos de empréstimos permitem que o capital emprestado seja amortizado por meio de um único pagamento ao final do período. Essa situação é descrita no denominado Sistema de Amortização Americano, a ser estudado mais adiante neste capítulo.
Saldo Devedor Representa o valor do principal da dívida, em determinado momento, após a dedução do valor já pago ao credor a título de amortização.
Prestação - É composto do valor da amortização mais os encargos financeiros devidos em determinado período de tempo. Assim:
Prestação = Amortização + Encargos Financeiros

Carência - Muitas operações de empréstimos e financiamentos preveem um diferimento na data convencional do início dos pagamentos. Por exemplo, ao se tomar um empréstimo por 4 anos, a ser restituído em prestações trimestrais, o primeiro pagamento ocorrerá normalmente três meses (um trimestre) após a liberação dos recursos, vencendo-se as demais ao final de cada um dos trimestres subsequentes. Pode, no entanto, ocorrer um diferimento (carência) no pagamento da primeira prestação, iniciando-se, por exemplo, 9 meses após o recebimento do capital emprestado. Neste caso, diz-se que a carência corresponde a dois trimestres, ou seja, ela equivale ao prazo verificado entre a data convencional de início de pagamento (final do primeiro trimestre) e a do final do 9º mês.

É importante acrescentar, ainda, que a carência significa a postergação só do principal, não sendo incluídos necessariamente os juros. Os encargos financeiros podem, dependendo das condições contratuais estabelecidas, serem pagos ou não durante a carência. É mais comum o pagamento dos juros durante o período de carência. Na hipótese de se decidir pela carência de juros, os mesmos são capitalizados e pagos juntos com a primeira parcela de amortização do principal ou distribuídos para as várias datas pactuadas de pagamento.

Exemplo Ilustrativo Geral - Visando ilustrar os principais sistemas de amortização normalmente adotados no mercado financeiro, admita, de uma maneira geral, um empréstimo com as seguintes condições básicas:

- Valor do Empréstimo = $100{.}000{,}00$
- Prazo da operação = 5 anos
- Taxa de Juros = $30\%$ ao ano (efetiva)

Sistema de Amortização Constante

O Sistema de Amortização Constante (SAC), como o próprio nome indica, tem como característica básica serem as amortizações do principal sempre iguais (ou constantes) em todo o prazo da operação. O valor da amortização é facilmente obtido mediante a divisão do capital emprestado pelo número de prestações.
Os juros, por incidirem sobre o saldo devedor cujo montante decresce após o pagamento de cada amortização, assumem valores decrescentes nos períodos.
Em consequência do comportamento da amortização e dos juros, as prestações periódicas e sucessivas do SAC são decrescentes em progressão aritmética.
Admita que o empréstimo de $ 100.000,00 descrito no Exemplo Geral deve ser pago, dentro de um prazo de 5 anos, em 10 prestações semestrais. Desconsiderando inicialmente a existência de um prazo de carência, pode-se elaborar a seguinte planilha financeira para a operação de empréstimo.

Períodos (semestres)	Saldo Devedor ($)	Amortização ($)	Juros ($)	Prestação ($)
0	100.000	-	-	-
1	90.000	100.000	14.017,50	24.017,50
2	80.000	10.000	12.615,80	22.615,80
3	70.000	10.000	11.214,00	21.214,00
4	60.000	10.000	9.812,30	19.812,30
5	50.000	10.000	7.008,80	17.008,80
6	40.000	10.000	7.008,80	17.008,80
7	30.000	10.000	5.607,00	15.607,00
8	20.000	10.000	4.205,30	14.205,30
9	10.000	10.000	2.803,50	12.803,50
10	-	10.000	1.401,80	11.401,80
Total	-	100.000	77.096,50	177.096,50

Conforme foi comentado, o SAC determina que a restituição do principal (capital emprestado) seja efetuada em parcelas iguais. Assim, o valor de cada amortização constante devida semestralmente é calculado pela simples divisão entre o principal ${$}100{.}000{,}00$ e o número fixado de prestações (10 semestres), ou seja: 

$${Amortização} = \frac{{Valor\ Emprestado}}{{Nº\ de Prestações}} = \frac{{$}100{.}000{,}00}{10} = {$}10{.}000 \mbox{/semestre}$$

Os pagamentos desses valores determinam, como é natural, decréscimos iguais e constantes no saldo devedor em cada um dos períodos, ocasionando ainda reduções nos valores semestrais dos juros e das prestações.
Para o cálculo dos juros trabalhou-se, como é mais comum nessas operações de crédito de médio e longo prazos, com a taxa equivalente composta. Assim, para uma taxa nominal de 30% ao ano, conforme considerada no Exemplo Ilustrativo Geral, a taxa equivalente semestral atinge:

Taxa Equivalente Semestral de 30% a.a.

$$\sqrt{1,30}-1 = 14,0175\% \mbox{a.s.}$$

$${Final do Primeiro semestre}$$