Ensino Superior

Juro

A matemática financeira trata, em essência, do estudo do valor do dinheiro ao longo do tempo. O seu objetivo básico é o de efetuar análises e comparações dos vários fluxos de entrada e saída de dinheiro de caixa verificados em diferentes momentos.

Receber uma quantia hoje ou no futuro não são evidentemente a mesma coisa. Em princípio, uma unidade monetária hoje é preferível à mesma unidade monetária disponível amanhã. Postergar uma entrada de caixa (recebimento) por certo tempo envolve um sacrifício, o qual deve ser pago mediante uma recompensa, definida pelos juros. Desta forma, são os juros que efetivamente induzem o adiamento do consumo, permitindo a formação de poupanças e de novos investimentos na economia.

Taxas de juros

A taxa de juros é o coeficiente que determina o valor do juro, isto é, a remuneração do fator capital utilizado durante certo período de tempo.
As taxas de juros se referem sempre a uma unidade de tempo (mês, semestre, ano etc.) e podem ser representadas equivalentemente de duas maneiras: taxa percentual e taxa unitária.

Taxa Percentual

$$ J = {$}1{.}000/100\times 20 = $$ $$ J = {$}10{,}00\times 20 = {$}200{,}00$$

O capital de ${$}1{.}000{,}00$ tem dez centos. Como cada um deles rende 20, a remuneração total da aplicação no período é, portanto de ${$}200{,}00.$

A transformação da taxa percentual em unitária se processa simplesmente pela divisão da notação em percentual por 100. Para a transformação inversa, basta multiplicar a taxa unitária por 100.

Taxa Percentual	Taxa Unitária
1,5%	0,015
8%	0,08
17%	0,17
86%	0,86
120%	1,20
1,500%	15,0

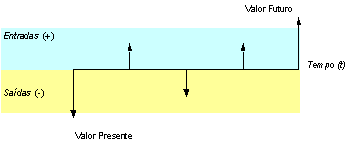
Diagrama do fluxo de caixa

Conforme foi comentado, a matemática financeira se preocupa com o estudo das várias relações dos movimentos monetários que se estabelecem em distintos momentos no tempo.

Estes movimentos monetários são identificados temporariamente através de um fluxo de caixa. O fluxo de caixa é de grande utilidade para as operações de matemática financeira, permitindo que se visualize no tempo o que ocorre com o capital. esquematicamente, pode ser apresentado da forma seguinte:

A linha horizontal registra a  escala de tempo, ou seja, o horizonte financeiro da operação. O ponto zero indica o momento inicial e os demais pontos representam os períodos de tempo (datas).

Fórmulas de Juros Simples

$$ J = C\times i\times n$$ onde J = valor dos juros expresso em unidades monetárias; C = Capital. i = taxa de juros, expressa em sua forma unitária; n = prazo. $$C= \frac{J}{i\times n}$$ $$i = \frac{J}{C\times n}$$ $$ n = \frac{J}{C\times i}$$

Exemplo:

1. Um capital de ${$}80{.}000{,}00$ é aplicado à taxa de $2{,}5$% ao mês durante um trimestre. Pede-se determinar o valor dos juros acumulados neste período.
Solução:
$$ J = C\times i\times n$$ $$J= 80{.}000{,}00\times 0{,}025\times 3$$ $$ J = {$}6{.}000{,}00$$

2. Um negociante tomou um empréstimo pagando uma taxa de juros simples de $6$% ao mês durante nove meses. Ao final deste período, calculou em ${$} 270{.}000{,}00$ o total de juros incorridos na operação. Determinar o valor do empréstimo.
Solução:
C=? i = 6% a.m. (0,06) n = 9 meses J = ${$}270{.}000$ $$C= \frac{J}{i\times n}$$ $$ C = \frac{270{.}000}{0{,}06\times 9} = \frac{270{.}000}{0{,}054}= {$} 500{.}000$$

3. Um capital de ${$} 40{.}000{,}00$ foi aplicado num fundo de poupança por 11 meses, produzindo um rendimento financeiro de ${$}9{.}680{,}00$. Pede-se apurar a taxa de juros oferecida por esta operação.

C = ${$}40{.}000{,}00$ i = ? n = 11 meses J = ${$}9{.}680{,}00$ $$ i = \frac{J}{C\times n}$$ $$ i = \frac{{$}9{.}680{,}00}{{$}40{.}000{,}00\times 11} = \frac{9{.}680{,}00}{440{.}000{,}}= $$ 0,022 ou 2,2% ao mês

4.Uma aplicação de ${$}250{.}000{,}00$ rendendo uma taxa de juros de 1,8% ao mês produz, ao final de determinado período juros no valor de ${$}27{.}000{,}00$. Calcular o prazo da aplicação.

C = ${$}250{.}000{,}00$ i = $1{,}8$% ao mês ${(}0{,}018{)}$ n = ? $J={$}27{.}000{,}00$ $$n=\frac{J}{C\times i}= \frac{27{.}000}{250{.}000\times 0{,}018}= \frac{27{.}000}{4{.}500}= 6\ {meses}$$

Montante e Capital

Um determinado capital, quando aplicado a uma taxa periódica de juro por determinado tempo, produz um valor acumulado determinado de montante, e identificado em juros simples por M. Em outras palavras, o montante é constituído do capital mais o valor acumulado dos juros, isto é:
$$M = C + J$$
No entanto, sabe-se que: $J = C\times i\times n$. Substituindo esta expressão básica na fórmula do montante supra, e colocando-se C em evidência:
$$M = C + C\times i\times n$$ $$M = C(1+i\times n)$$
A expressão $\left(1 + i \times n\right)$ é definida como fator de capitalização (ou de valor futuro -CFS) dos juros simples. Ao multiplicar um capital por este fator, corrige-se o seu valor para uma data futura, determinando o montante. O inverso, ou seja, $\frac{1}{1+i\times n}$ é denominado de fator de atualização (ou de valor presente FAS). Ao se aplicar o fator sobre um valor expresso em uma data futura, apura-se o seu equivalente numa data atual.


Exemplos
1. Uma pessoa aplica ${$} 18{.}000{,}00$ à taxa de 1,5% ao mês durante 8 meses. Determinar o valor acumulado ao final deste período.
Solução:
$C ={$}18{.}000{,}00$
i = 1,5% ao mês (0,015)
n = 8 meses
M = ? $$ M = C(1+i\times n)$$ $$ M = {$} 18{.}000{,}00 (1 + 0{,}015\times 8)$$ $$ M = 18{.}000\times 1{,}12 = {$}\ 20{.}160{,}00$$

Taxa proporcional e taxa equivalente

Por exemplo, para uma taxa de juros de 18% ao ano, se a capitalização for definida mensalmente (ocorrerão 12 vezes juros no período de um ano), o percentual de juros que incidirá sobre o capital a cada mês será:
$$Taxa Proporcional = \frac {18\%}{12}=1{,}5\%\ ao\ mês$$
As taxas de juros simples se dizem equivalentes quando, aplicadas a um mesmo capital e pelo mesmo intervalo de tempo, produzem o mesmo volume linear de juros.
Por exemplo, em juros simples, um capital de ${$}500{.}000{,}00$, se aplicado a 2,5% ao mês ou 15% ao semestre pelo prazo de um ano, produz o mesmo montante linear de juros. Isto é:
$$J(2,5\% a.m.) = {$}500{.}000{,}00\times 0{,}025\times 12 = {$}150{.}000{,}00$$ $$J(15\% a.s.) = {$}500{.}000{,}00\times 0{,}15\times 2 = {$} 150{.}000{,}00$$

Exemplos:

1. Calcular a taxa anual proporcional a: (a) 6% ao ano; (b) 10% ao bimestre.
Solução:
$$ a) i = 6\%\times 12 = 72\%\ ao\ ano$$ $$ b) i = 10\%\times 6 = 60\%\ ao\ ano$$

2. Calcular a taxa de juros semestral proporcional a: (a) 60% ao ano; (b) 9% ao trimestre.
Solução:
$$a) i = \frac{60\%}{12}\times 6 = 30\%\ a.s. \quad pois: \frac{12}{6} = \frac{60}{30}$$ $$\frac{12}{6} = \frac{60}{i}$$ $$ 12i = 60\times 6$$ $$12i = 360$$ $$i = 30$$ $$b) i = \frac{9\%}{3}\times 6 = 18\%\ a.s. \quad ou: i = 9\%\times 2 = 18\%\ a.s.$$

Juro Exato e Juro Comercial

É comum nas operações de curto prazo, onde predominam as aplicações com taxas referenciadas em juros simples, ter-se o prazo definido em número de dias. Nesses casos, o número de dias pode ser calculado de duas maneiras:
a) pelo tempo exato, utilizando-se efetivamente o calendário do ano civil (365 dias). O juro apurado desta maneira denomina-se juro exato;
b) pelo ano comercial, o qual admite o mês com 30 dias e o ano com 360 dias. Tem-se por este critério, a apuração do denominado juro comercial ou ordinário.
Por exemplo, 12% ao ano equivale, pelos critérios enunciados, à taxa diária de:
a) Juro Exato: $$ \frac {12\%}{365 dias} = 0{,}032877\% ao\ dia$$
b) Juro Comercial:$$ \frac {12\%}{360\ dias} = 0{,}033333\%\ ao\ dia$$
Na ilustração, o juro comercial diário é ligeiramente superior ao exato pelo menor número de dias considerado no intervalo de tempo.

Equivalência Financeira

O problema da equivalência financeira constitui-se no raciocínio básico da matemática financeira. Conceitualmente, dois ou mais capitais representativos de uma certa data dizem-se equivalentes quando, a uma certa taxa de juros, produzem resultados iguais numa data comum.
Por exemplo, ${$}120{,}00$ vencíveis daqui a um ano e ${$}100{,}00$, hoje, são equivalentes a uma taxa de juros simples de $20\%$, uma vez que os ${$}100{,}00$ capitalizados, produziriam ${$}120{,}00$ dentro de um ano, ou os ${$}120{,}00$, do final do primeiro ano, resultariam em ${$}100{,}00$ se atualizados para hoje. Ou seja, ambos os capitais produzem, numa data de comparação (data focal) e taxa de $20\%$ ano ano, resultados idênticos.
Exemplos: 1. Determinar se ${$}438{.}080{,}00$ vencíveis daqui a 8 meses é equivalente se receber hoje ${$}296{.}000{,}00$, admitindo uma taxa de juros simples de $6\%$ ao mês.
Solução:
Data Focal = 8 $$M= 296{.}000\times (1 + 0{,}06\times 8)$$
Data Focal = 0(zero):
$$C=\frac{438{.}080{,}00}{(1+0{,}06\times 8)}$$
Os capitais são equivalentes à taxa de $6\%$ ao mês. Portanto, a esta taxa de juros é indiferente receber ${$}296{.}000{,}00$ hoje ou $438{.}080{,}00$ daqui a 8 meses.

Os capitais A1, A2 e B1, B2 e B3 dizem-se equivalentes se, quando expressos em valores de uma data comum (data de comparação ou data focal), e a mesma razão de juros, apresentam resultados iguais. Sendo a data de comparação o momento $0$, tem-se:
$$\frac{A1}{(1+i\times 1)}+ \frac{A2}{(1+i\times 2)}=\frac{B1}{(1+i\times 3)}+\frac{B2}{(1+i\times 4)}+\frac{B3}{(1+i\times 5)}$$

Juros Compostos

O regime de juros compostos considera que os juros formados em cada período são acrescidos ao capital formando o montante (capital mais juros) do período. Este montante, por sua vez, passará a render juros no período seguinte formando um novo montante (constituído do capital inicial, dos juros acumulados e dos juros sobre os juros formados em períodos anteriores), e assim por diante. Este processo de formação dos juros é diferente daquele descrito para os juros simples, onde unicamente o capital rende juros, não ocorrendo remuneração sobre os juros formados em períodos anteriores. Tecnicamente o regime de juros compostos é superior ao de juros simples, principalmente pela possibilidade de fracionamento dos prazos, conforme foi introduzido no capítulo anterior. No critério composto, a equivalência de capitais pode ser apurada em qualquer data, retratando melhor a realidade das operações que o regime linear.

Fórmulas de juros compostos

Para melhor desenvolver este conceito e definir suas fórmulas de cálculo, admita ilustrativamente uma aplicação de ${$}1{.}000{,}00$ a taxa composta de $10\%$ ao mês. Identificando-se por PV o valor presente (capital) e FV o valor futuro (montante), tem-se os seguintes resultados ao final de cada período:

Final do 1º mês: o capital de ${$}1{.}000{,}00$ produz resultados de ${$}100{,}00$ ($10\%\times {$}1{.}000)$ e um montante de ${$}1{.}100{,}00 (1{.}000{,}00 + 100{,}00)$, ou seja:
$$FV = 1{.}000{,}00\times (1 + 0{,}010)= {$}1{.}100{,}00$$

Final do 2º mês: o montante do mês anterior ${$}1{.}100{,}00$ é o capital deste 2º mês, servindo de base para o cálculo de juros deste período. Assim:

$$FV= 1{.}000{,}00\times (1+0{,}10)\times (1+0{,}10)$$ $$FV = 1{.}000{,}00\times (1+0{,}10)^2 = {$}1{.}210{,}00$$

Generalizando:
$$FV = PV\times(1+i)^n$$ $$PV = \frac{FV}{(1+i)^n}$$

Onde $(1+i)^n$ é o fator de capitalização (ou de valor futuro), - FCC(i,n) a juros compostos, e $\frac{1}{(1+i)^n}$ o fator de atualização (ou de valor presente) - FAC(i,n) a juros compostos.

Por outro lado, sabe-se que o valor monetário dos juros (J) é apurado pela diferença entre o montante (FV) e o capital (PV), podendo-se obter seu resultado também pela seguinte expressão: $$J = FV - PV$$

Como: $FV = PV(1+i)^n$
Colocando-se PV em evidência:
$$J = PV\times [(1+i)^n - 1]$$

Exemplo: 1. Se uma pessoa deseja obter ${$}27{.}500{,}00$ dentro de um ano, quanto deverá ela depositar hoje numa alternativa de poupança que rende $1{,}7\%$ de juros compostos ao mês?
Solução:
FV = ${$}27{.}500{,}00$ n = 1 ano (12 meses); i = 1,7% ao mês PV = ? $$PV = \frac{FV}{(1+i)^n}= \frac{27{.}500{,}00}{(1+0{,}017)^{12}}= \frac{27{.}500{,}00}{(1{,}017)^{12}}$$ $$PV = \frac{27{.}500{,}00}{1{,}224197}= {$} 22{.}463{,}70$$
De fato, uma aplicação de ${$}22{.}463{,}70$ hoje, a $1{,}7\%$ a.m. de juros compostos, produz ao final de um ano o montante de ${$}27{.}500{,}00$, ou seja:
$$FV = 22{.}463{,}70\times (1{,}017)^{12}= {$} 27{.}500{,}00$$

2. Qual o valor de resgate de uma aplicação de ${$}12{.}000{,}00$ em um título pelo prazo de 8 meses à taxa de juros composta de $3,5\%$ a.m.?
Solução:
$$FV= PV(1+i)^n = 12{.}000\times(1+0{,}035)^8 = 12{.}000\times 1{,}316809 = {$} 15{.}801{,}71$$
3. Determine a taxa mensal composta de uma aplicação de ${$}40{.}000{,}00$ que produz um montante de ${$}43{.}894{,}63$ ao final de um quadrimestre.
Solução:
$$FV = PV(1+i)^n$$ $$\frac{FV}{PV}=(1+i)^4$$ $$\frac{43{.}894{,}63}{40{.}000{,}00}=(1+i)^4$$ $$1{,}097366 = (1+i)^4$$ $$\sqrt[4]{1{,}097366}= \sqrt[4]{(1+i)^4}$$ $$1+i = 1{,}0235$$ $$i = 0{,}0235\ ou\ 2{,}35\% {a.m.}$$

4. Uma aplicação de ${$}22{.}000{,}00$ efetuada em certa data produz, à taxa composta de juros de $2{,}4\%$ ao mês, um montante de ${$}26{.}596{,}40$ em certa data futura. Calcular o prazo da operação.
$$FV = PV(1+i)^n$$ $$\frac{FV}{PV}=(1+i)^n$$ $$\frac{26{.}596{,}40}{22{.}000{,}00}=(1{,}024)^n$$ $$1{,}208927 = (1{,}24)^n$$
Aplicando logaritmos, tem-se:
$${log} 1{,}208927 = n\times {log} 1{,}024$$ $$n = \frac{{log}1{,}208927}{{log}1{,}024}= \frac{0{,}082400}{0{,}010300}= 8\ {meses}$$

Taxas Equivalentes

Ao se tratar de juros simples, foi comentado que a taxa equivalente é a própria taxa proporcional da operação. Por exemplo, a taxa de $3\%$ ao mês e $9\%$ ao trimestres são ditas proporcionais, pois mantêm a seguinte relação:
$$\begin{matrix} \underbrace{ \frac{1}{3} } \\ {Prazos} \end{matrix}= \begin{matrix} \underbrace{ \frac{3}{9} } \\ {Taxas}\end{matrix}$$
São também equivalentes, pois promovem a igualdade dos montantes de um mesmo capital ao final de certo período de tempo. Por exemplo, em juros simples um capital de ${$}80{.}000{,}00$ produz o mesmo montante em qualquer data se capitalizado a $3\%$ a.m. e $9\%$ a.t.


$$n = 3 meses \begin{cases} FV(3\%{a.m.}) = 80{.}000{,}00(1+0{,}03\times 3) = {$}87{.}200{,}00 \\ FV(9\%{a.t.})= 80{.}000{,}00(1+0{,}09\times 1) = {$}87{.}200{,}00 \end{cases}$$
$$n= 12 meses \begin{cases} FV(3\%{a.m.}) = 80{.}000{,}00(1+0{,}03\times 12) = {$}87{.}200{,}00 \\ FV(9\%{a.t.})= 80{.}000{,}00(1+0{,}09\times 4) = {$}87{.}200{,}00 \end{cases}$$
O conceito enunciado de taxa equivalente permanece válido para o regime de juros compostos diferenciando-se, no entanto, a fórmula de cálculo da taxa de juros. Por se tratar de capitalização exponencial, a expressão da taxa equivalente composta é a média geométrica da taxa de juros do período inteiro, isto é:
$$i_q= \sqrt[q]{1+i}-1$$
onde: q = número de períodos de capitalização.
Exemplo: A taxa equivalente composta mensal de $10{,}3826\%$ é de $1{,}66\%$ ou seja:
$$i_6= \sqrt[6]{1+0{,}103826}-1$$ $$i_6= \sqrt[6]{1{,}103826}-1 = 1{,}0166-1 = 0{,}0166\ ou\ 1{,}66\% {a.m.}$$

Taxa nominal e taxa efetiva

A taxa efetiva de juros é a taxa de juros apurada durante todo o prazo n, sendo formada exponencialmente através dos períodos de capitalização. Ou seja, a taxa efetiva é o processo de formação dos juros pelo regime de juros compostos ao longo dos períodos de capitalização. É obtida pela seguinte expressão:
$${Taxa\ Efetiva}({i_f}) = (1+i)^q -1$$
onde q representa o número de períodos de capitalização dos juros.
Por exemplo, uma taxa de $3{,}8\%$ ao mês determina um montante efetivo de juros de $56,45\%$ ao ano, ou seja:
$${Taxa\ Efetiva}({i_f}) = (1+i)^q -1$$ $$i_f = (1+0{,}038)^{12}-1 = 56{,}44\% {a.a.}$$

Descontos

Entende-se por valor nominal o valor de resgate, ou seja, o valor definido para um título em sua data de vencimento. Representa, em outras palavras, o próprio montante da operação.
A operação de se liquidar um título antes de seu vencimento envolve geralmente uma recompensa, ou um desconto pelo pagamento antecipado. Desta maneira, desconto pode ser entendido como a diferença entre o valor nominal de um título e o seu valor atualizado apurado n períodos antes de seu vencimento.
Por outro lado, o valor descontado de um título é o seu valor atual na data do desconto, sendo determinado pela diferença entre o valor nominal e o desconto, ou seja:
Valor Descontado = Valor Nominal - Desconto

As operações de desconto podem ser realizadas tanto sob o regime de juros simples como no de juros compostos.

Descontos Racionais (ou "por dentro")

O desconto racional, também denominado de desconto "por dentro", incorpora os conceitos e relações básicas de juros simples, conforme desenvolvidos no primeiro capítulo.
Assim, sendo $D_ r$ o valor do desconto racional, C o capital (ou valor atual), i a taxa periódica de juros e n o prazo do desconto (número de períodos que o título é negociado antes de seu vencimento), tem-se a conhecida expressão de juros simples:
$$D_r=C\times i\times n$$
Pela própria definição de desconto e introduzindo-se o conceito de valor descontado no lugar de capital no cálculo do desconto, tem-se:
$$D_r=N-V_r$$
sendo N o valor nominal (ou valor de resgate, ou montante) e $V_r$ o valor descontado (ou valor atual) na data da operação. Como:
$$V_r=C= \frac{N}{1+i\times n}$$
tem-se:
$$D_r=N- \frac{N}{1+i\times n}=\frac{N(1+i\times n)-N}{1+i\times n}= \frac{N+N\times i\times n-N}{1+i\times n}$$ $$D_r= \frac{N\times i\times n}{1+i\times n}$$
Já o valor descontado, conforme definição apresentada, é obtido pela seguinte expressão de cálculo:

$$V_r=N-D_r$$ $$V_r=N- \frac{N\times i\times n}{1+i\times n}$$ $$V_r = \frac{N(1+i\times n)-N\times i\times n}{1+i\times n}$$ $$= \frac{N+N\times i\times n - N\times i\times n}{1+i\times n}$$
$$V_r = \frac{N}{1+i\times n}$$

Observe, uma vez mais, que o desconto racional representa exatamente as relações de juros simples descritas no capítulo inicial. É importante registrar que o juro incide sobre o capital (valor atual) do título, ou seja, sobre o capital liberado da operação. A taxa de juro (desconto) cobrada representa, dessa maneira, o custo efetivo de todo o período do desconto.

Exemplos:
1. Seja um título de valor nominal de $4{.}000{,}00$ vencível em um ano, que está sendo liquidado 3 meses antes de seu vencimento. Sendo de $42\%$ a.a. a taxa nominal de juros corrente, pede-se calcular o desconto e o valor descontado desta operação.

Solução:
Desconto

$$D_r= \frac{N\times i\times n}{1+i\times n}$$ $$D_r= \frac{4{.}000\times 0{,}035\times 3}{1+0{,}035\times 3}= \frac{420{,}00}{1{,}105}={$}380{,}00$$

Valor Descontado
$$V_r= N-D_r$$ $$V_r = 4{.}000{,}00-380{,}10 = {$}3{.}619{,}90$$
Ou:
$$V_r = \frac{N}{1+i\times n}= \frac{4{.}000{,}00}{1+0{,}035\times 3}= {$}3{.}619{,}90$$

Do ponto de vista do devedor $380{,}10$ representam o valor que está deixando de pagar por saldar a dívida antecipadamente (3 meses antes de seu vencimento). O valor líquido do pagamento (valor descontado) é de $3{.}619{,}90$

Desconto bancário (ou comercial, ou "por fora")

Este tipo de desconto, simplificadamente por incidir sobre o valor nominal (valor de resgate) do título, proporciona maior volume de encargos financeiros efetivos nas operações. Observe que, ao contrário dos juros "por dentro", que calculam os encargos sobre o capital efetivamente liberado na operação, ou seja, sobre o valor presente, o critério "por fora" apura os juros sobre o montante, indicando custos adicionais ao tomador de recursos.
A modalidade de desconto "por fora" é amplamente adotada pelo mercado, notadamente em operações de crédito bancário e comercial a curto prazo.
O valor deste desconto, genericamente denominado desconto "por fora" $(D_f)$, no regime de juros simples é determinado pelo produto do valor nominal do título (N), da taxa de desconto periódica "por fora" contratada na operação (d) e do prazo de antecipação definido para o desconto (n). Isto é:

$$D_F = N\times d\times n$$

O valor descontado "por fora" $(V_F)$, aplicando-se a definição, é obtido:

$$V_F=N-D_F$$ $$V_F = N-N\times d\times n\qquad \longrightarrow V_F = N(1-d\times n)$$
Exemplo:
1. Seja um título de valor nominal de ${$}4{.}000{,}00$ vencível em um ano, que está sendo liquidado antes de seu vencimento. Sendo de $42\%$ a.a. a taxa de desconto adotada, pede-se calcular o desconto e o valor descontado desta operação.
Solução:

Desconto
$$D_F=N\times d\times n$$ $$D_F= 4{.}000{,}00\times 0{,}035\times 3 \qquad \longrightarrow D_F = 420{,}00$$
Observe que o maior valor dos juros cobrado pelo título deve-se ao fato, conforme ressaltado anteriormente, de o desconto "por fora" ser aplicado diretamente sobre o valor nominal (valor de resgate) e não sobre o valor atual como é característico das operações de desconto racional.

Em verdade, o valor do desconto "por fora" aquivale, num mesmo momento do tempo, ao montante do desconto "por dentro", supondo-se as mesmas condições de prazo e taxa. Isto é:

$$D_r = {$}380{,}10$$ $$D_F = {$}420{,}00$$

Para uma taxa de $3{,}5\%$ a.m. e um período de desconto de 3 meses, conforme estabelecido na ilustração, tem-se:

$$D_F = D_r(1+i\times n)$$ $$D_F= 380{,}10\times(1+0{,}035\times 3) = 380{,}00\times (1{,}105) \longrightarrow D_F = {$}420{,}00$$

O cálculo do valor descontado $(V_F)$ é desenvolvido:

$$V_F = N(1-d\times n)$$ $$V_F = 4{.}000{,}00\times(1-0{,}035\times 3)$$ $$V_F = 4{.}000{,}00\times (0{,}895) \\ V_F = {$}3{.}580{,}00$$

Torna-se evidente que o devedor desse título, descontado pelo desconto bancário (ou comercial, ou "por fora"), assume encargos maiores que aqueles declarados para a operação.

A taxa de juros efetiva desta operação não equivale à taxa de desconto utilizada. Note que, se são pagos ${$}420{,}00$ de juros sobre um valor atual de ${$}3{.}580{,}00$, a taxa de juros assume o seguinte percentual efetivo:

$$i = \frac{{$}420{,}00}{{$}3{.}580{,}00}= 11{,}73\%\quad {ao\ trimestre}$$